Chapter 24 Electric Potential Review Ap Physics C

Chapter 24. Electric Potential 24. 1. What is Physics? 24. two. Electric Potential Energy 24. three. Electric Potential 24. 4. Equipotential Surfaces 24. 5. Computing the Potential from the Field 24. 6. Potential Due to a Point Accuse 24. 7. Potential Due to a Group of Indicate Charges 24. viii. Potential Due to an Electric Dipole 24. 9. Potential Due to a Continuous Charge Distribution 24. 10. Calculating the Field from the Potential 24. 11. Electric Potential Energy of a Organisation of Bespeak Charges 24. 12. Potential of a Charged Isolated Usher

What is Physics? • Gravitational force: F=Gm ane m ii/r 2 • Electrostatic force: F=Gq 1 q 2/r 2 • One thing is in mutual: both of these forces are conservative
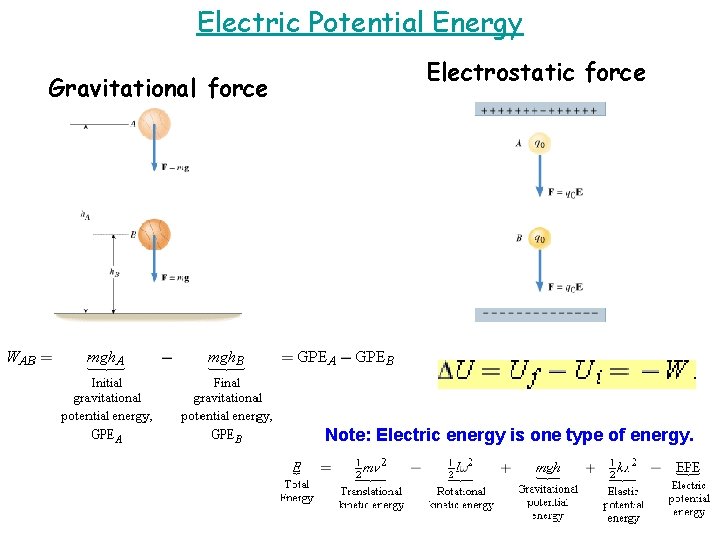
Electric Potential Energy Gravitational force Electrostatic strength Note: Electrical energy is ane type of energy.

Reference Point of Electrical Potential Energy The reference signal can be anywhere. For convenience, nosotros usually fix charged particles to be infinitely separated from one another to be zero potential free energy The potential energy U of the system at any point f is where W∞ is the piece of work done by the electric field on a charged particle as that particle moves in from infinity to point f.

Example 1 A proton, located at bespeak A in an electrical field, has an electric potential energy of UA = 3. twenty × 10 -19 J. The proton experiences an boilerplate electric forcefulness of 0. 80 × 10 -nine Due north, directed to the right. The proton so moves to indicate B, which is a distance of 1. 00 × 10 -10 m to the right of point A. What is the electrical potential energy of the proton at point B ?

Electric Potential The electric potential V at a given point is the electric potential energy U of a small test charge q 0 situated at that point divided past the charge itself: If nosotros set at infinity as our reference potential energy, SI Unit of Electric Potential: joule/coulomb=volt (V) Notation: • Both the electric potential free energy U and the electric potential V are scalars. • The electric potential energy U and the electric potential V are not the same. The electric potential energy is associated with a test charge, while electric potential is the property of the electric field and does not depend on the test charge.

The Electric Potential Difference The electric potential divergence between whatever ii points i and f in an electric field. • It is equal to the divergence in potential free energy per unit charge betwixt the two points. • the negative work washed by the electric field on a unite accuse equally that particle moves in from point i to point f. Annotation: • Only the differences ΔV and ΔU are measurable in terms of the piece of work W. • The is ΔV belongings of the electrical field and has nothing to do with a test charge • The mutual proper name for electric potential difference is "voltage".
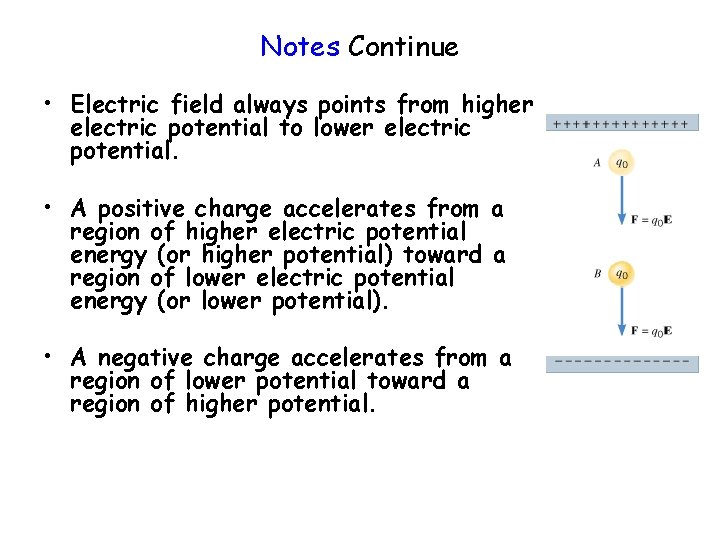
Notes Continue • Electric field e'er points from higher electric potential to lower electric potential. • A positive accuse accelerates from a region of higher electrical potential free energy (or higher potential) toward a region of lower electric potential energy (or lower potential). • A negative accuse accelerates from a region of lower potential toward a region of higher potential.

Conceptual Example The Accelerations of Positive and Negative Charges Iii points, A, B, and C, are located forth a horizontal line, as Effigy nineteen. 4 illustrates. A positive test charge is released from rest at A and accelerates toward B. Upon reaching B, the test accuse continues to accelerate toward C. Assuming that only motion along the line is possible, what will a negative exam charge do when it is released from residuum at B?

Example 2 Work, Electric Potential Energy, and Electrical Potential The work done past the electrical strength as the test charge (q 0=+two. 0× 10– 6 C) moves from A to B is WAB=+v. 0× x– 5 J. (a) Find the departure, ΔU=UB–UA, in the electric potential energies of the accuse between these points. (b) Determine the potential deviation, ΔV=VB–VA, between the points.

Instance 3 Operating a Headlight Determine the number of particles, each conveying a charge of 1. lx× 10– nineteen C (the magnitude of the charge on an electron), that pass between the terminals of a 12 -V machine bombardment when a threescore. 0 -Westward headlight burns for one hour.
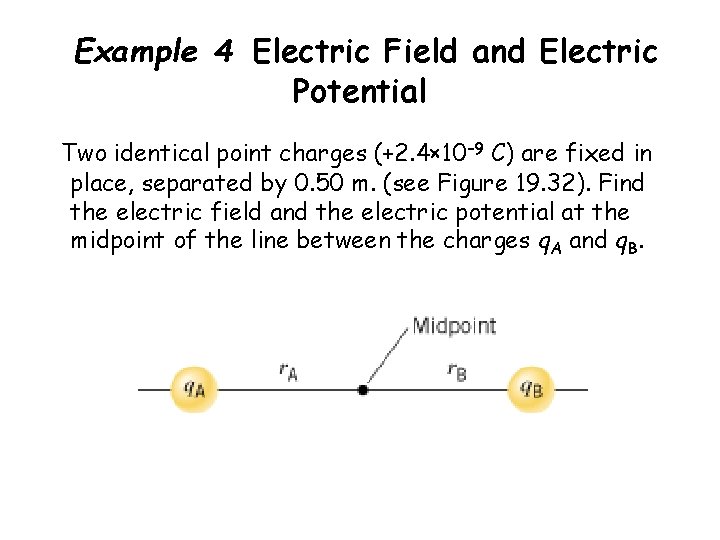
Example 4 Electrical Field and Electric Potential Two identical indicate charges (+two. 4× 10– nine C) are fixed in identify, separated by 0. 50 m. (see Effigy 19. 32). Find the electric field and the electric potential at the midpoint of the line between the charges q. A and q. B.

Equipotential Surfaces An equipotential surface is a surface on which the electric potential is the same everywhere.

Relation of Equipotential Surfaces and the Electric Field 1. The internet electric force does no piece of work as a accuse moves on an equipotential surface. 2. The electric field created past any charge or group of charges is everywhere perpendicular to the associated equipotential surfaces and points in the direction of decreasing potential. What volition happen if the electrical field E is non perpendicular to the equipotential surface?
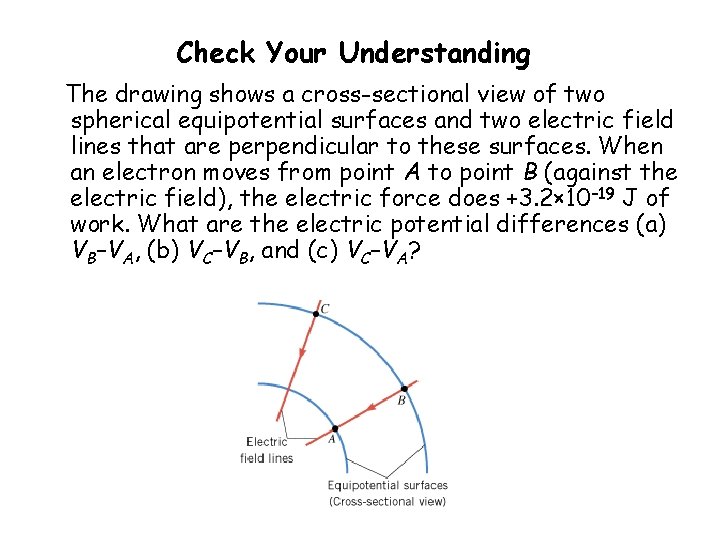
Check Your Understanding The drawing shows a cross-sectional view of two spherical equipotential surfaces and two electrical field lines that are perpendicular to these surfaces. When an electron moves from point A to indicate B (against the electric field), the electric force does +3. 2× 10– 19 J of piece of work. What are the electrical potential differences (a) VB–VA, (b) VC–VB, and (c) VC–VA?

Computing the Potential from the Field

Calculating the Field from the Potential The potential gradient gives the component of the electric field along the displacement Δs
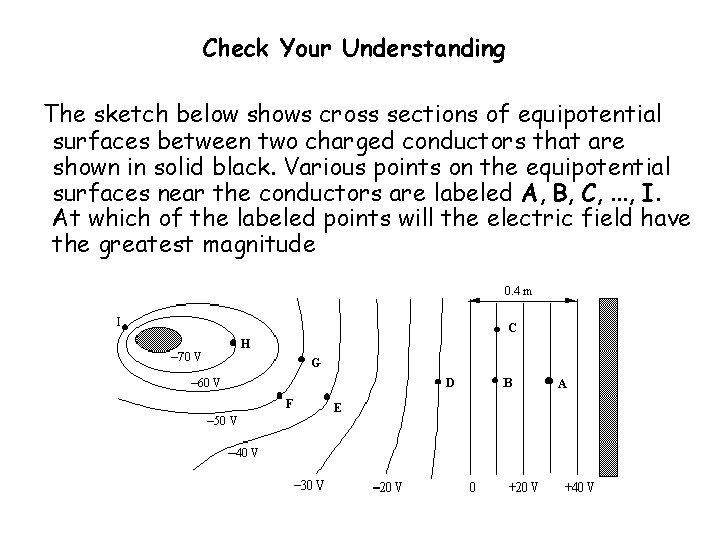
Bank check Your Understanding The sketch below shows cross sections of equipotential surfaces between 2 charged conductors that are shown in solid black. Diverse points on the equipotential surfaces near the conductors are labeled A, B, C, . . . , I. At which of the labeled points will the electrical field take the greatest magnitude

Example 4 The metallic contacts of an electric wall socket are almost ane. 0 cm apart and are maintained at a potential difference of 120 5. What is the average electrical field strength between the contacts? What is the direction of the electric field if the left contact is the college potential? The lower potential? Treat the potential divergence between the contacts every bit being constant in time.

Sample Problem The electrical potential at any bespeak on the fundamental axis of a uniformly charged disk is given by Eq. 24 -37 , Starting with this expression, derive an expression for the electric field at any indicate on the axis of the deejay.
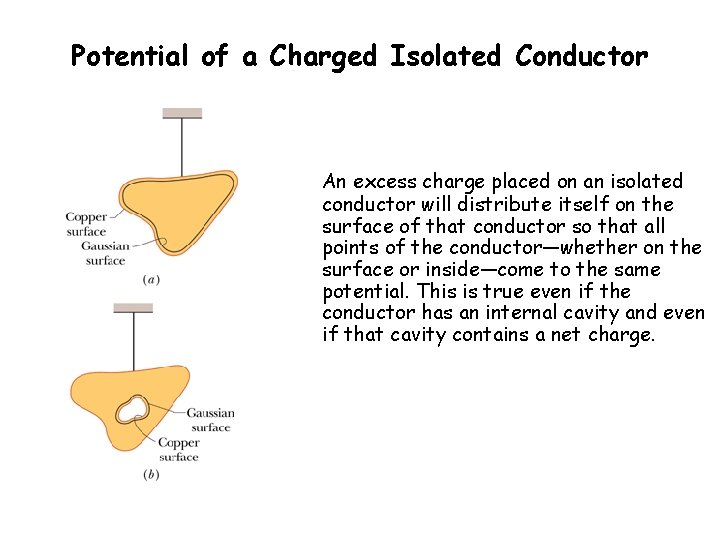
Potential of a Charged Isolated Conductor An excess charge placed on an isolated conductor will distribute itself on the surface of that conductor so that all points of the conductor—whether on the surface or inside—come to the aforementioned potential. This is true even if the conductor has an internal cavity and even if that cavity contains a net charge.

Isolated Usher in an External Electric Field • The free conduction electrons distribute themselves on the surface in such a style that the electrical field they produce at interior points cancels the external electric field that would otherwise be there. • The electron distribution causes the internet electrical field at all points on the surface to exist perpendicular to the surface.
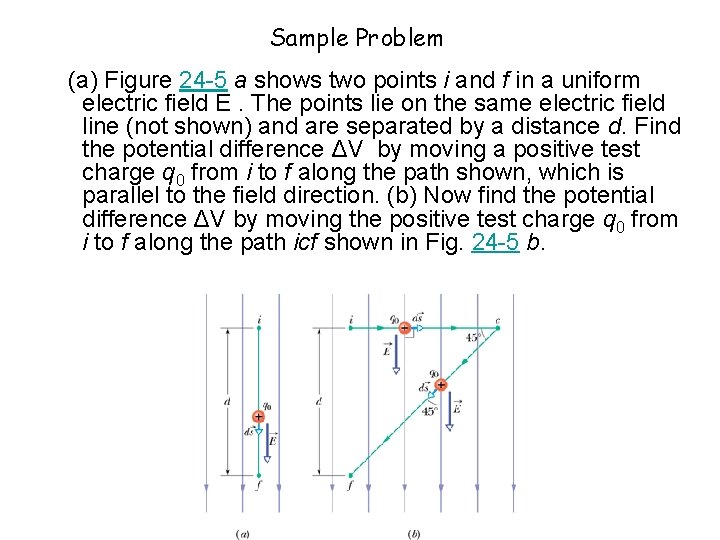
Sample Problem (a) Figure 24 -five a shows two points i and f in a uniform electric field Due east. The points prevarication on the aforementioned electrical field line (not shown) and are separated past a distance d. Find the potential deviation ΔV by moving a positive examination charge q 0 from i to f along the path shown, which is parallel to the field management. (b) Now find the potential difference ΔV by moving the positive examination charge q 0 from i to f along the path icf shown in Fig. 24 -5 b.
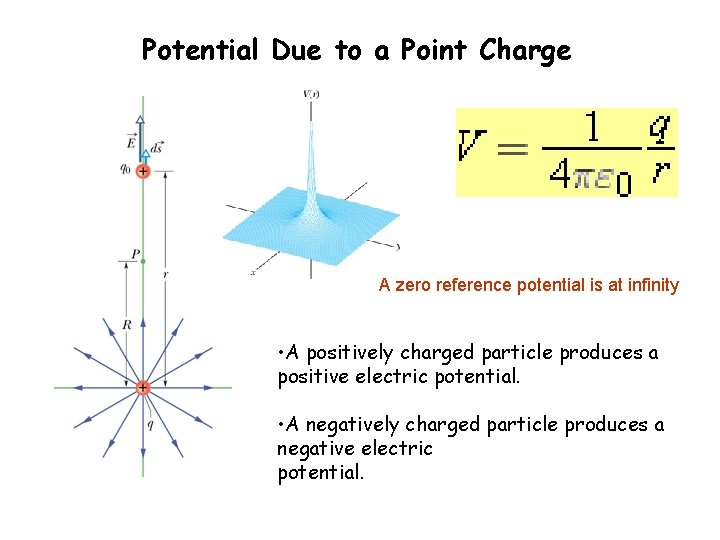
Potential Due to a Bespeak Accuse A cipher reference potential is at infinity • A positively charged particle produces a positive electric potential. • A negatively charged particle produces a negative electric potential.

Potential Due to a Group of Betoken Charges The potential at a point due to any number of point charges can exist found past simply finding the potential at the point due to each lone and adding the potentials: Vtot=Five 1+5 2+∙∙∙+VN

Potential Due to an Electric Dipole
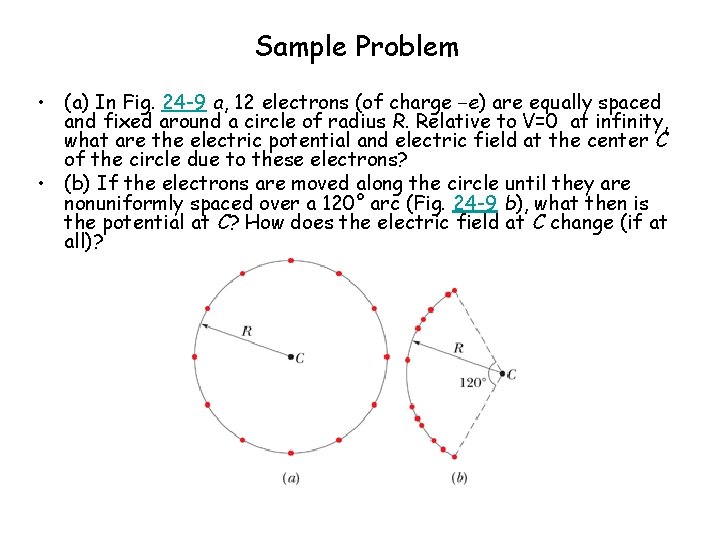
Sample Trouble • (a) In Fig. 24 -9 a, 12 electrons (of charge −e) are every bit spaced and fixed effectually a circle of radius R. Relative to V=0 at infinity, what are the electric potential and electrical field at the center C of the circumvolve due to these electrons? • (b) If the electrons are moved along the circle until they are nonuniformly spaced over a 120° arc (Fig. 24 -9 b), what then is the potential at C? How does the electric field at C alter (if at all)?

Potential Due to a Continuous Accuse Distribution
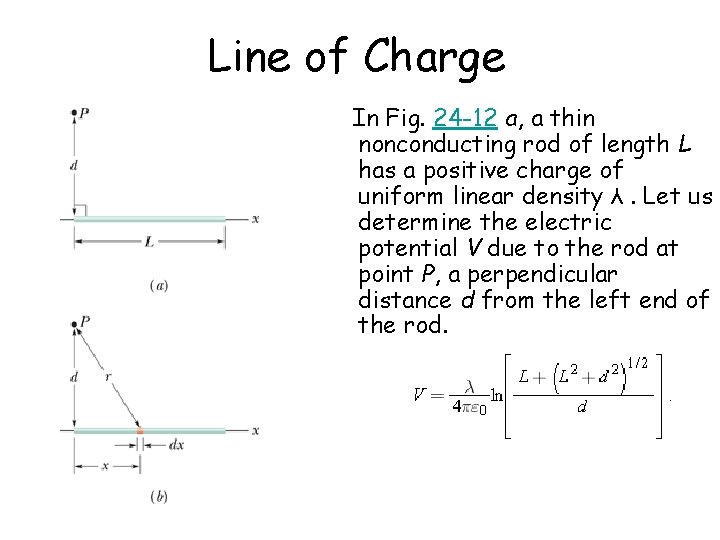
Line of Charge In Fig. 24 -12 a, a sparse nonconducting rod of length 50 has a positive accuse of uniform linear density λ. Let us decide the electric potential 5 due to the rod at point P, a perpendicular distance d from the left end of the rod.
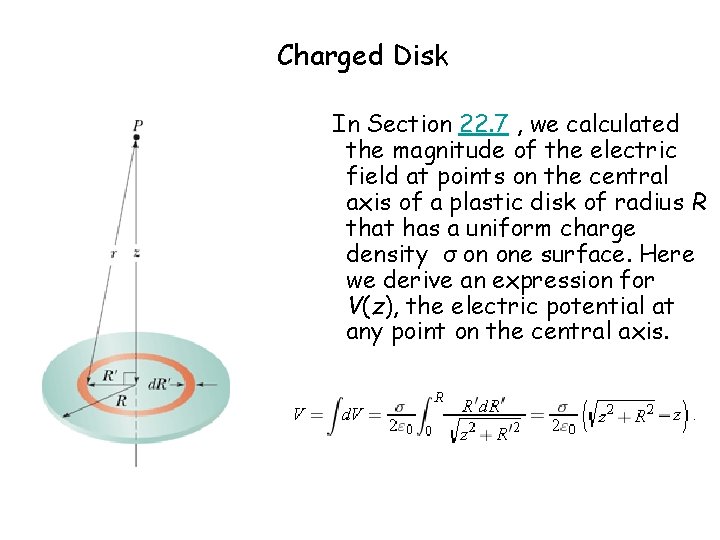
Charged Disk In Department 22. seven , we calculated the magnitude of the electrical field at points on the primal axis of a plastic deejay of radius R that has a uniform accuse density σ on ane surface. Here we derive an expression for 5(z), the electric potential at any point on the primal axis.

Electrical Potential Energy of a System of Indicate Charges The electrical potential free energy of a organization of fixed point charges is equal to the piece of work that must be done past an external agent to assemble the system, bringing each charge in from an infinite distance.
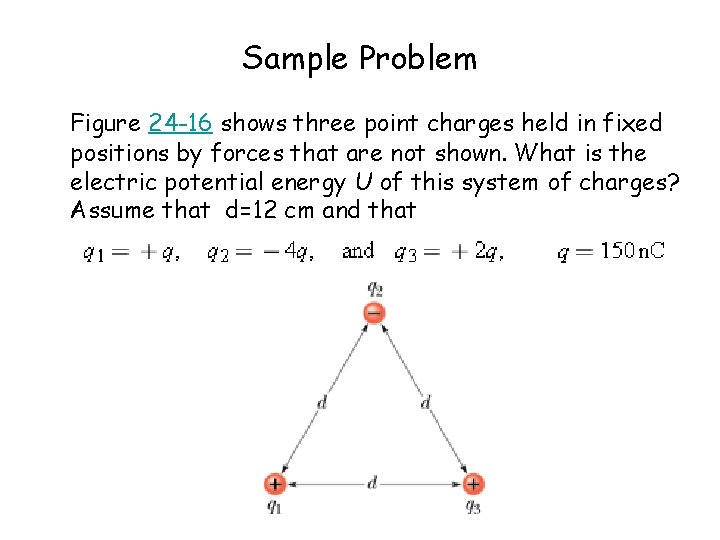
Sample Problem Figure 24 -16 shows three betoken charges held in fixed positions by forces that are non shown. What is the electric potential free energy U of this system of charges? Assume that d=12 cm and that

Conceptual Questions i. The drawing shows 3 possibilities for the potentials at ii points, A and B. In each example, the same positive accuse is moved from A to B. In which case, if any, is the near work washed on the positive charge by the electrical force? Account for your answer.

2. The electrical field at a unmarried location is zero. Does this fact necessarily mean that the electric potential at the same identify is zero? Use a spot on the line betwixt 2 identical signal charges as an instance to back up your reasoning. 3. The potential is constant throughout a given region of space. Is the electric field goose egg or nonzero in this region? Explain. four. In a region of infinite where the electric field is constant everywhere, is the potential constant everywhere? Account for your answer.

5. A positive exam charge is placed in an electric field. In what direction should the charge be moved relative to the field, such that the charge experiences a constant electrical potential? Explain. 6. The potential at a point in space has a certain value, which is not zero. Is the electrical potential energy the same for every accuse that is placed at that point? Give your reasoning.
Source: https://slidetodoc.com/chapter-24-electric-potential-24-1-what-is/
0 Response to "Chapter 24 Electric Potential Review Ap Physics C"
Post a Comment